Thermal effects#

This page covers the model of beam heating influence on the deposit shape and presents utilised solution for the heat equation.

Temperature dependence#

The influence of the beam heating effect through temperature increase is multifold.

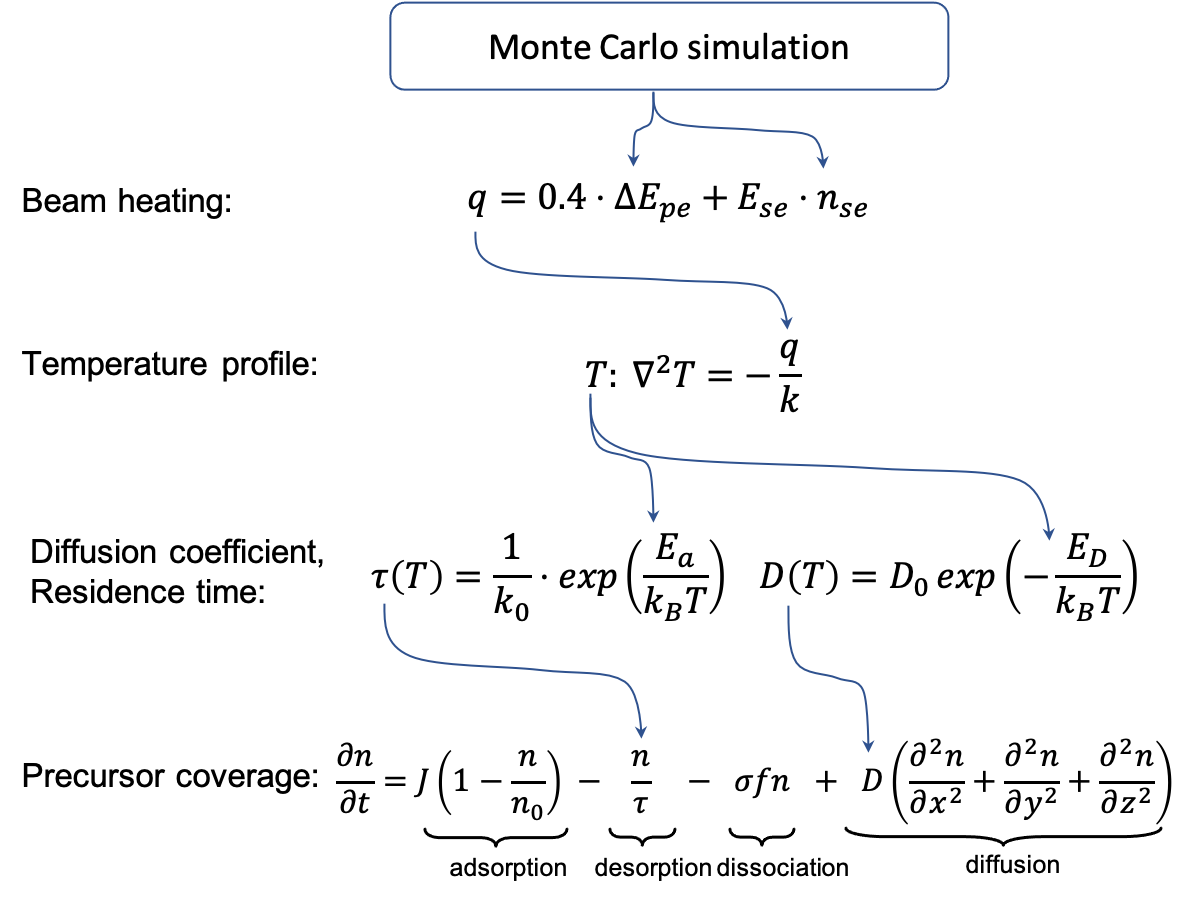
_images/temperature_influence_diagram.png

Initially, the heating power of the beam 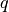$q$ is generated by the Monte Carlo module.

After that, a temperature profile is derived based on 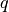$q$ and thermal conductivity of the deposit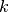 $k$

The temperature profile is then used to calculate surface profiles of residence time and diffusion coefficient.

Finally, those profiles are used for the calculation of the precursor coverage profile. Precursor coverage then directly affects the amount of the deposited material.

Heat equation#

Both heat distribution and diffusion are described via a parabolic PDE equation and thus require a numerical solution.

Although, the processes are similar in nature, they occur at characteristic time steps differing by orders of magnitude. This fact implies usage of different numerical solution for th heat transfer problem.

In the actual version of the package, the default for heat transfer is SOR.

The heat equation:

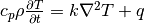$c_p\rho\frac{\partial T}{\partial t}=k\nabla^2T+q$ ,

which is resolved in 3D space:

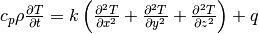
$c_p\rho\frac{\partial T}{\partial t}= k\left(\frac{\partial^2T}{\partial x^2}+\frac{\partial^2T}{\partial y^2}+\frac{\partial^2T}{\partial z^2}\right)+q$

where:

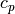$c_p$ is the heat capacity of the solid medium $\left[ \frac{J}{kg\cdot K} \right ]$

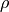$\rho$ is the density $\left[ \frac{kg}{nm^3} \right ]$

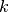$k$ is thermal conductance $\left[ \frac{W}{nm\cdot K} \right ]$

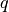$q$ is the heating source originating from electron beam heating $\left[ \frac{J}{nm^3} \right ]$

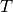$T$ is temperature [K]

Due to the fact, that heat transfer characteristic time step is orders of magnitude shorter than one of mass transport (diffusion), the solution of heat equation requires an accordingly shorter time step. Such fine time discretization would make the simulation orders of magnitude slower.

Although, the same feature of the heat transfer means that evolution of an equilibrium or steady state occurs almost instantly [Mutunga2019]. It means that time discretization is neglected and the problem simplifies to a calculation of a steady state:

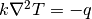
$k\nabla^2T=-q$

The problem of deriving a steady state is called a relaxation problem and is solved by a family of relaxation methods. Here it is solved via a Simultaeous Over-Relaxation (SOR) method. Generally, it represents an FTCS scheme, ultimately applied with the maximum stable time step. The main prerequisition for the SOR method is convergence of the solution. The convergence is evaluated based on a norm of the difference between current and previous iterations. When the norm diminishes below a certain value that is called solution accuracy the convergence is reached.

Due to the slow rise of temperature caused by beam heating, a steady state profile can be derived at a significantly lower rate than the diffusion equation is solved.

Effectively, re-calculation of the steady state temperature profile is necessary approximately 10 times per deposition time second for the PtC deposit.

[Mutunga2019]

Mutunga E., Winkler R., Sattelkow J. et al., Impact of Electron-Beam Heating during 3D Nanoprinting, ACS Nano 2019, 13, 5198-5213